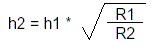

Last modified: 2007-02-10 by phil nelson
Keywords: flag area |
Links: FOTW homepage |
search |
disclaimer and copyright |
write us |
mirrors
See also:
We start with the basics. Lets have a flag, for now let us consider it rectangular with the height equal h and length equal l, that makes it area equal A = h * l. Let us define the ratio as R = l/h.
The requirement that two flags displayed together have equal area could then be made so:
A1 = h1 * l1 or A1 = (h12) * R1
and similarly
A2 = h2 * l2 or A2 = (h22) * R2
A1 = A2 gives us easily that the height of the second flag should be:
That was easy, but this does not take into account the visual "feeling" that is effect of the flag flying in the wind. Now until here things were quite clear mathematically, but henceforward I take some assumptions and hypothesis.
Let us assume that the area of a flag flying in the wind as perceived by the observer depends only on the amount of the wind blowing. The stronger the wind the lesser the "wrinkling" and therefore the "virtual area" would be close to the area of the still flag on surface. The simplest function to emulate this following the natural laws would be exponential one, like this:
A' = A * f(v) = A * (1-e(-av))
where v is the speed on the wind and a is the "perception coefficient"; - a value that would have to be experimentally determined.
For large values of the perceptions coefficient, the value of virtual area A' approaches the still flag area A.
The answer to the practical question how "big" a flag one should hoist beside the first flag so they appear the same, what interests us is the size of the hoist of the second flag:
The wind speed is the same in both flags, of course. The last expression might be simplified a bit further I guess, but it is a bit too late right now.
If we assume for the moment that a1 = a2, i.e.. that the perception coefficient is equal for all flag, the last expression becomes equal to 1, so the whole expression becomes the same as the one for the "still flags".
However, we know that the flags of different shapes do not necessarily make the same perception of "shortening" when flying, so in general a1 < > a2.
It is reasonable to assume that the value of a depends only on the shape of the flag. In reality this may not be so, it may depend on the materials the flags are made of, the ways the flag is stitched together, if it contains heavy emblems in the fly and so on, but this may all be ignored for the first approximation or if we assume that both flags in question are made of the same materials and, for example, silk-screen printed so that the design of the flag has no effect on the issue. (That the flags are being hoisted in the same mechanical method on the same kind of masts is an assumption that I have silently taken from the very beginning!)
In general, the value may be defined also for non rectangular flag.
If the value of a depends of the shape of the flag, in case of the rectangular flags that would mean that a is a function of the ratio
a = g(R)
After some thinking I assume that the longer flags appear less "shortened" in the slow wind conditions then the short flags. If I have not made an error in computation (this is a call for verification), the lesser shortening for the longer flags would be expressed with larger values of coefficient a. The simplest assumption would be that the dependence is linear:
a = p * R
If this is so then p could be proved itself to be some kind of an universal perceptional constant. This may well prove to be an important vexillological number.
(If possibly simplification of the last part of the expression could be useful)
This states what we have known that the height of the second flag depends on the ratios of the two flags and on the wind.
Željko Heimer, 18 July 2004